|
E' l'ultima spiaggia: se proprio non e' possibile fare nient'altro, con questo metodo potrai almeno ottenere una soluzione approssimata. Rimandando al capitolo Analisi numerica per l'analisi dell'approssimazione vediamo qui un semplice esempio del metodo; Per seguire il metodo devi conoscere bene la geometria cartesiana e devi saper tracciare i grafici delle principali funzioni Vediamo il metodo su un semplice esempio risolvere log x + x = 0 per log x intendiamo il logaritmo naturale di x: log x = ln x = loge x cerchiamo di separare l'espressione in due funzioni di cui conosciamo i grafici una prima ed una dopo l'uguale log x = -x La soluzione cercata sara' l'ascissa del punto di intersezione delle due funzioni (o anche punto comune alle due funzioni) y= -x 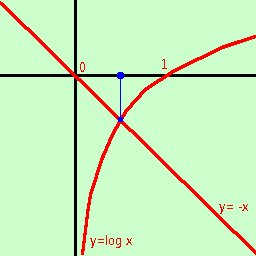
E' sufficiente ora tracciare i grafici delle due funzioni La prima e' la funzione logaritmo la seconda e' la bisettrice del secondo e quarto quadrante La soluzione (il punto blu piu' grosso) e' compresa fra 0 ed 1 e vale circa 0,4 |

|

|

|

|