|
Vediamo quindi quali sono le formule per trovare il volume del prisma retto 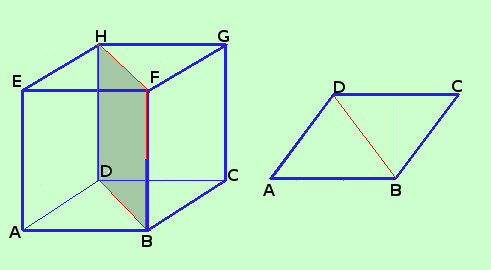 Partiamo dal volume del parallelepipedo retto: la sua base e' un parallelogramma. Sappiamo dalla geometria del piano che la diagonale di un parallelogramma lo divide in parti uguali Se quindi consideriamo il piano passante per tale diagonale e per i due spigoli laterali adiacenti, esso divide il parallelepipedo in due prismi retti congruenti (ABDEFH) e (BCDFGH) I due prismi, essendo congruenti avranno lo stesso volume (che vale meta' del volume del parallelepipedo di partenza) Quindi, siccome l'area di base di un prisma retto triangolare e' meta' dell'area del parallelogramma avremo anche per il suo volume V = Asb·h 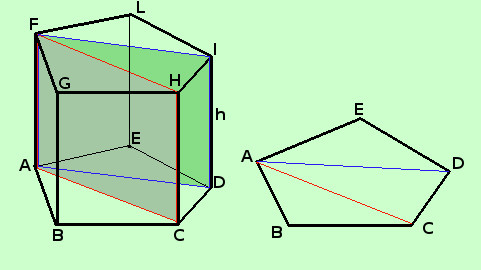
Ora, considerando un qualunque prisma retto, preso un vertice di base e congiungendo tale vertice con i restanti vertici di base dividiamo la base in triangoli. se per ogni diagonale della base cosi' costruita consideriamo il piano formato da tale diagonale e dagli spigoli laterali adiacenti alla diagonale stessa, dividiamo il prisma in prismi retti triangolari Allora il suo volume sara' dato dalla somma dei volumi dei prismi componenti V = V1 + V2 + V3 + ...... V = Asb1·h +Asb2·h +Asb3·h + .... e raccogliendo h V = (Asb1 + Asb2 +Asb3 + ....)·h Ma sommando le aree dei triangoli di base otteniamo l'area della figura di base quindi
Il volume del prisma retto si trova moltiplicando l'area del poligono di base per la misura dell'altezza Come esempio nella figura a lato ho preso un prisma retto pentagonale che viene suddiviso in tre prismi retti triangolari aventi la stessa altezza h |

|

|

|

|