|
si chiama delle proiezioni perche' e' come se se proiettiamo due lati del triangolo sul terzo lato Con questo teorema conoscendo due lati e due angoli posso trovare il terzo lato: non e' che sia molto esaltante, anche perche' i dati sono sovrabbondanti (2 lati e 2 angoli) pero' servira' per dimostrare il teorema di Carnot Teorema:
a = b cos b = a cos c = a cos Dimostriamo la prima relazione 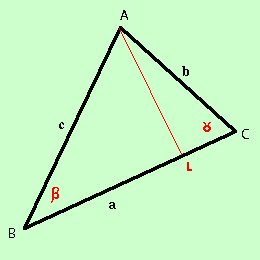 dal punto A mando la perpendicolare AL sul lato BC ottengo i due triangoli ABL e ALC il triangolo ABL e' rettangolo e quindi, per il teorema del coseno sui triangoli rettangoli abbiamo BL = AB cos Anche il triangolo ACL e' rettangolo quindi, per lo stesso teorema, abbiamo LC = AC cos ma noi abbiamo che BC = a = BL + LC = c cos come volevamo Dimostriamo la seconda relazione 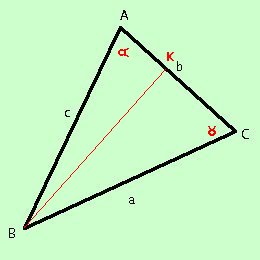 dal punto B mando la perpendicolare BK sul lato AC ottengo i due triangoli ABK e BKC il triangolo ABK e' rettangolo e quindi, per il teorema del coseno sui triangoli rettangoli abbiamo AK = AB cos Anche il triangolo BKC e' rettangolo quindi, per lo stesso teorema, abbiamo KC = BC cos ma noi abbiamo che AC = b = AK + KC = c cos come volevamo Dimostriamo la terza relazione 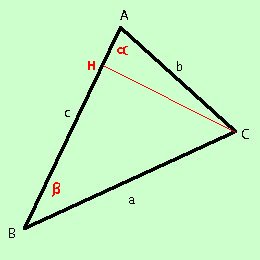 dal punto C mando la perpendicolare CH sul lato AB ottengo i due triangoli ACH e CHB il triangolo ACH e' rettangolo e quindi, per il teorema del coseno sui triangoli rettangoli abbiamo AH = AC cos Anche il triangolo CHB e' rettangolo quindi, per lo stesso teorema, abbiamo HB = CB cos ma noi abbiamo che AB = c = AH + HB = b cos come volevamo |
||||

|

|

|

|