Applicazioni a disequazioni quoziente di espressioni di primo e secondo grado Siccome il quoziente si comporta, per i segni, come il prodotto quando hai un quoziente devi pensare che ogni quoziente e' equivalente a piu' sistemi di disequazioni Ad esempio se hai x - 3 --------------------- x2 - 6x + 5    > 0 siccome devi trovare dove il quoziente e' maggiore di zero potrai considerare le soluzioni che vanno bene per i due sistemi x-3 > 0                   x-3 < 0 x2 - 6x + 5 > 0            x2- 6x + 5 < 0 Infatti se numeratore e denominatore dell'espressione sono entrambe positivi oppure entrambe negativi allora l'espressione prodotto e' positiva Se invece hai: x - 3 --------------------- x2 - 6x + 5    < 0 siccome devi trovare dove il quoziente e' minore di zero potrai considerare le soluzioni che vanno bene per i due sistemi x - 3 > 0                   x - 3 < 0 x2 - 6x + 5 < 0            x2 - 6x + 5 > 0 Infatti se numeratore e denominatore dell'espressione hanno segno contrario allora l'espressione e' negativa la regola dei segni del quoziente e' identica a quella per il prodotto Anche qui, senza dover risolvere piu' sistemi, pero', e' piu' semplice porre sia il numeratore che il denominatore maggiori di zero (sia che l'espressione sia maggiore che minore di zero) e poi controllare dove il prodotto dei segni di queste espressioni risulta positivo oppure negativo. (Cio' equivale a risolvere contemporaneamente tutti i sistemi) Vediamo come esempio la soluzione di una disequazione Risolvere (x-3)(x2 - 6x + 5) < 0 Anche se devo trovare i valori minori di zero pongo entrambe i fattori maggiori di zero x - 3 > 0 x2 - 6x + 5 > 0 la prima x - 3 > 0 e' verificata per x > 3 la seconda   x2 - 6x + 5 > 0   e' verificata per    x < 1 U x > 5       Calcoli quindi il mio sistema e' equivalente al sistema x > 3 x < 1 U x > 5 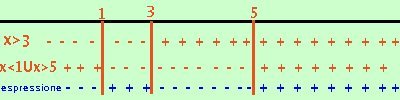Riporto su un grafico, evidenziando con un piu' dove il fattore e' positivo e con un meno dove e' negativo. Nella riga in blu metto il segno dell'espressione prodotto Ora faccio i calcolo dei segni: siccome devo prendere dove l'espressione e' negativa l'espressione prodotto sara' negativa dove numeratore e denominatore hanno segni diversi Per distinguere questo caso dalla soluzione di un sistema io preferisco indicare i valori positivi con un piu' e quelli negativi con un meno, mentre nel sistema ho indicato con una riga continua le soluzioni accettabili e con una linea tratteggiata quelle non accettabili Pero' stai attento a non confonderti perche' qualche libro di testo indica nello stesso modo (riga continua e tratteggiata) sia la soluzione di un sistema che la soluzione di una disequazione prodotto di espressioni La soluzione e' x < 1   U   3 < x < 5 Importante! Un caso da prendere bene in considerazione e' quando abbiamo la frazione 0 oppure 0 vediamolo su alcuni esercizi x2 - 9 --------------------- x - 2    0           svolgimento x2 -3x + 2 --------------------- x - 5    0           svolgimento Importante e' anche il seguente caso particolare: quando il numeratore ed il denominatore sono fra loro semplificabili x2 -5x + 6 --------------------- x - 3    > 0           svolgimento